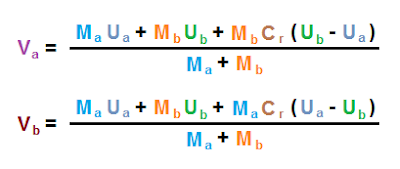In addition to gravity pulling bodies together, atmospheric drag affecting bodies near each other, and friction for bodies in contact, I wanted to accurately model the impact of bodies - collisions.
There are 3 types of collisions:
Elastic - Partial bounce (some stick). The degree of elasticity is called the coefficient of restitution, a value between 0.0 and 1.0. The higher the coefficient, the more the bounce.
Perfectly Elastic - No loss of kinetic energy, perfect bounce. The coefficient of restitution is 1.0. In reality there are no perfectly elastic collisions but billiard balls impacting are a rough real world example.
Perfectly Inelastic (Plastic) - Bodies stick together upon impact. The coefficient of restitution is 0.0.
Ua = Primary Body Approach Speed
Ub = Secondary Body Approach Speed
Ma = Primary Body Mass
Mb = Secondary Body Mass
Cr = Coefficient of Restitution, 0 = Inelastic, 1 = Elastic
Va = Primary Body Departure Speed
Vb = Secondary Body Departure Speed
https://en.wikipedia.org/wiki/Collision
https://en.wikipedia.org/wiki/Elastic_collision
https://en.wikipedia.org/wiki/Inelastic_collision
https://en.wikipedia.org/wiki/Coefficient_of_restitution
Orbital Aero Code - update()
A refresher of our update() function in the OrbitalAeroModel class.
// Primary function to process the physics and kinematics all bodies.
bool OrbitalAeroModel::update(double timeStep_seconds)
{
// It's important all forces are calculated before all positions are updated before all collisions
// are checked, etc. That way the order in which bodies are looped through does not affect how they
// affect other bodies in space.
// Calculate Motor Thrust (From control system and motor abilities.)
// Sum all the forces acting on every body, including forces from thrust, gravity, atmospheric drag,
// and friction.
processForces();
// Can now translate and rotate each body.
processKinematics(timeStep_seconds);
// After moving the body, check for collisions and adjust positions/velocities as appropriate.
processCollisions(timeStep_seconds);
return true;
}
Orbital Aero Code - processCollisions()
// Handle collisions between bodies.
bool OrbitalAeroModel::processCollisions(double timeStep_seconds)
{
// Loop through all bodies and check for collisions.
// Unlike the forces calculations, not every body needs to be run through in the secondary loop.
// For example, if you have 4 bodies, the following loops will process as follows:
// Primary 1 Secondary 2
// Primary 1 Secondary 3
// Primary 1 Secondary 4
// Primary 2 Secondary 3
// Primary 2 Secondary 4
// Primary 3 Secondary 4
// Primary loop is through all bodies.
map <uint64, BodyModel>::iterator iteratorPrimaryBody = tableBodies.begin();
while (iteratorPrimaryBody != tableBodies.end())
{
BodyModel &primaryBody = iteratorPrimaryBody->second;
if (primaryBody.active)
{
// Secondary loop begins one after the primary body iterator.
map <uint64, BodyModel>::iterator iteratorSecondaryBody = iteratorPrimaryBody;
iteratorSecondaryBody++;
// Continue the secondary loop to the end of the bodies list.
while (iteratorSecondaryBody != tableBodies.end())
{
BodyModel &secondaryBody = iteratorSecondaryBody->second;
if (secondaryBody.active && (&primaryBody != &secondaryBody))
{
// Calculate the distance betweeen bodies.
Vector relativeDistance_meters = secondaryBody.location_meters - primaryBody.location_meters;
double relativeDistanceMagnitude_meters = relativeDistance_meters.magnitude();
double combinedRadii_meters = primaryBody.radius_meters + secondaryBody.radius_meters;
// Do the bodies occupy the same space?
if (relativeDistanceMagnitude_meters < combinedRadii_meters && relativeDistanceMagnitude_meters > 0)
{
// Potential impact. Get elevation at that location (convert to geodetic).
// Not loading terrain yet, just do the impact.
// Coefficient of Restitution
// 0 = Perfectly Plastic, objects remain together
// 1 = Perfectly Elastic, kinetic energy conserved / bounce
double Cr = 0.5;
// Primary body impacting secondary body.
//
// Approach--> \ |
// \ |
// \ | <-- Surface
// Normal--> /_____\|
// \ /|
// / |
// / |
// Departure--> |/_ |
//
// Take the dot product of the velocity vector with the normal surface to get the magnitude of the impact speed.
Vector vectorNormalToImpact = -relativeDistance_meters.unit();
double primaryBodyPerpendicularApproachSpeed_metersPerSecond = Vector::dotProduct(primaryBody.velocity_metersPerSecond, vectorNormalToImpact);
double secondaryBodyPerpendicularApproachSpeed_metersPerSecond = Vector::dotProduct(secondaryBody.velocity_metersPerSecond, vectorNormalToImpact);
// Determine departure speeds based on coefficient of restitution, perpendicular speeds, and masses.
// Va = (Ma * Ua + Mb * Ub + Mb * Cr * (Ub - Ua)) / (Ma + Mb)
// Vb = (Ma * Ua + Mb * Ub + Ma * Cr * (Ua - Ub)) / (Ma + Mb)
// Ua = Primary Body Approach Speed
// Ub = Secondary Body Approach Speed
// Ma = Primary Body Mass
// Mb = Secondary Body Mass
// Cr = Coefficient of Restitution, 0 = Inelastic, 1 = Elastic
// Va = Primary Body Departure Speed
// Vb = Secondary Body Departure Speed
double primaryBodyPerpendicularDepartureSpeed_metersPerSecond =
(primaryBody.massTotal_kilograms() * primaryBodyPerpendicularApproachSpeed_metersPerSecond +
secondaryBody.massTotal_kilograms() * secondaryBodyPerpendicularApproachSpeed_metersPerSecond +
secondaryBody.massTotal_kilograms() * Cr * (secondaryBodyPerpendicularApproachSpeed_metersPerSecond - primaryBodyPerpendicularApproachSpeed_metersPerSecond)) /
(primaryBody.massTotal_kilograms() + secondaryBody.massTotal_kilograms());
Vector primaryPerpendicularChange_metersPerSecond = vectorNormalToImpact * (primaryBodyPerpendicularDepartureSpeed_metersPerSecond - primaryBodyPerpendicularApproachSpeed_metersPerSecond);
primaryBody.velocity_metersPerSecond += primaryPerpendicularChange_metersPerSecond;
double secondaryBodyPerpendicularDepartureSpeed_metersPerSecond =
(primaryBody.massTotal_kilograms() * primaryBodyPerpendicularApproachSpeed_metersPerSecond +
secondaryBody.massTotal_kilograms() * secondaryBodyPerpendicularApproachSpeed_metersPerSecond +
primaryBody.massTotal_kilograms() * Cr * (primaryBodyPerpendicularApproachSpeed_metersPerSecond - secondaryBodyPerpendicularApproachSpeed_metersPerSecond)) /
(primaryBody.massTotal_kilograms() + secondaryBody.massTotal_kilograms());
Vector secondaryPerpendicularChange_metersPerSecond = vectorNormalToImpact * (secondaryBodyPerpendicularDepartureSpeed_metersPerSecond - secondaryBodyPerpendicularApproachSpeed_metersPerSecond);
secondaryBody.velocity_metersPerSecond += secondaryPerpendicularChange_metersPerSecond;
// Reposition the entities based on the "bounce".
primaryBody.location_meters += primaryBody.velocity_metersPerSecond * timeStep_seconds;
secondaryBody.location_meters += secondaryBody.velocity_metersPerSecond * timeStep_seconds;
// Recalculate the distance, ensure we're still not occupying the same space.
Vector relativeDistanceAfterMovement_meters = secondaryBody.location_meters - primaryBody.location_meters;
double relativeDistanceAfterMovementMagnitude_meters = relativeDistanceAfterMovement_meters.magnitude();
if (relativeDistanceAfterMovementMagnitude_meters < combinedRadii_meters)
{
// Still occupying the same space, reposition the less dense mass outside.
Vector unitVectorToIntercept = relativeDistanceAfterMovement_meters.unit();
if (primaryBody.massBase_kilograms > secondaryBody.massBase_kilograms)
{
secondaryBody.location_meters = primaryBody.location_meters + (unitVectorToIntercept * (combinedRadii_meters + 0.01));
}
else
{
primaryBody.location_meters = secondaryBody.location_meters + (-unitVectorToIntercept * (combinedRadii_meters + 0.01));
}
}
} // (relativeDistanceMagnitude_meters < combinedRadii_meters && relativeDistanceMagnitude_meters > 0)
} // ((secondaryBody.active) && (primaryBody.index != secondaryBody.index))
iteratorSecondaryBody++;
} // (iteratorSecondaryBody != tableBodies.end())
} // (primaryBody.active)
iteratorPrimaryBody++;
} // (iteratorPrimaryBody != tableBodies.end())
return true;
}
Results
Two bodies impacting with a coefficient of restitution of 1.0
Two bodies impacting with a coefficient of restitution of 0.5
Two bodies impacting with a coefficient of restitution of 0.0
How about a game of billiards?
Ball approaching (slightly off angle)...
After impact...
And finally impacting something with a much higher mass...
Copyright (c) 2016 Clinton Kam
Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.